Matthew N. Bernstein

Matthew N. Bernstein

Computational Biologist at Immunitas Therapeutics

True understanding is “seeing” in 3D

3 minute read

Published:

In this post, I will discuss an analogy that I find useful for thinking about what it means to “understand” something: True understanding of a concept is akin to “seeing” the concept in its native three-dimensional space, whereas partial understanding is merely seeing a two-dimensional projection of that inherently three-dimensional concept.

One of the most important and, in my opinion, overlooked skill sets in academics is that of understanding the state of one’s own knowledge. That is, to understand what you really truly know versus what you only partially know. Without this skill, it is difficult to address gaps in your understanding.

In this post, I’ll provide an analogy that I find helpful for thinking about what it means to “understand”. This analogy also helps guide my teaching goals.

The analogy goes as follows: An abstract, complex concept is akin to an object that resides in three-dimensional (3D) space. True understanding of that concept is akin to seeing the object in 3D. One only partially understands the concept if they are only able to see the object as a two-dimensional (2D) projection. A 2D viewing of a concept is understanding a concept through limited perspectives. One fully understands the concept when they are able to make the leap from viewing the object in 2D to seeing the object in 3D. This leap is often accompanied by an “aha” moment.

This analogy is well illustrated by the image on the cover of Gödel, Escher, Bach by Douglas Hofstadter:

drawing

In this image, the 3D wooden blocks ares the abstract concept. The various 2D projections are various ways that one can approach or view the concept; however, they are inherently incomplete. True understanding of the concept is akin to seeing the wooden blocks as they are, and being able to mentally manipulate the 3D wooden blocks.

As a toy example, I will use the concept of Shannon’s information entropy, which I have discussed in a previous blog post. As I discussed in that post, there are multiple ways to view the concept of information entropy of a categorical distribution:

  1. As the expected self-information over all of the possible events that may occur when sampling from the distribution.
  2. As a measure of “uniformness” or “uncertainty” of the distribution.
  3. As the minimal expected number of bits required to communicated samples drawn from the distribution, as discussed in my post discussing Shannon’s Source Coding Theorem.

Each of these perspectives are akin to a 2D projection:

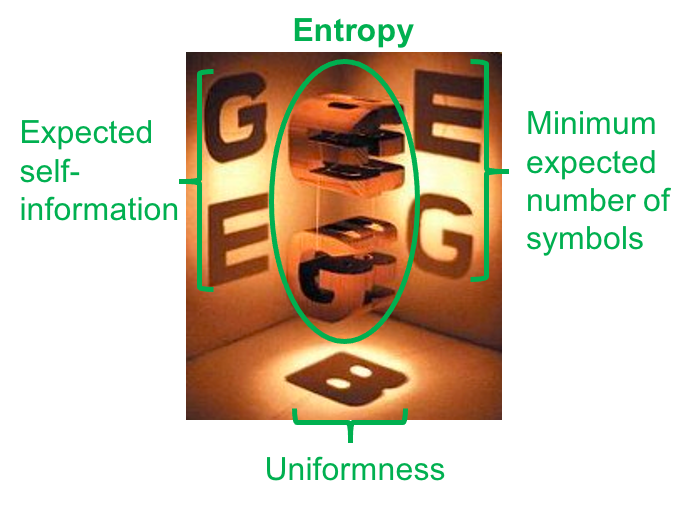
drawing

However, each of these 2D projections (i.e, perspectives) is incomplete. If you only understand entropy through one of these perspectives, then your understanding is incomplete. Truly understanding the concept of entropy is to intuit how all of these perspectives are really just projections of some “higher dimensional” concept that integrates all of these ideas.

Importantly, the sum of multiple 2D projections does not equate to seeing the full 3D object. There is something phenomenologically different about seeing the 3D object than seeing an amalgamation of 2D projections. It is their integration that results in understanding.

When teaching a concept such as this one, it often must be approached through 2D projections first. Jumping straight to the 3D object is often too challenging. However, through explaining and exploring multiple 2D projections of the concept, the student will begin to construct the 3D object in their mind. When self-learning, I take this same approach: I first try to grasp the various 2D projections; however, I am not satisfied until those 2D projections begin to integrate together into a 3D object. Once I am able to mentally manipulate that 3D object at will (i.e., rotate it and form new 2D projections onto new hyperplanes), then I know that I really grasp the concept.

You May Also Enjoy

Assessing the utility of data visualizations based on dimensionality reduction

14 minute read

Published:

We human beings use our vision as our chief sense for understanding the world, and thus when we are confronted with data, we try to understand that data through visualization. Dimensionality reduction methods, such as PCA, t-SNE, and UMAP, are approaches designed to enable the visualization of high-dimensional data. Unfortunately, because these methods inevitably distort aspects of the data, these methods are receiving new scrutiny. In this post, I propose that dimensionality reduction requires a “probabilistic” framework of interpretation rather than a “deterministic” one wherein conclusions one draws from a dimensionality reduction plot have some probability of not actually being true of the data. I will propose that this does not mean these plots are not useful. Rather, to evaluate their utility, I will argue that empirical user studies of these methods will shed light on whether these methods provide more benefit or more harm in practice.

The invertible matrix theorem

14 minute read

Published:

Throughout my blog posts on linear algebra, we have proven various properties about invertible matrices. In this post we bring, all of these statements into a single location and form a set of statements called the “invertible matrix theorem”. Each statement in the invertible matrix theorem proves that the matrix is invertible and implies all of the rest of the statements.

Median-ratio normalization for bulk RNA-seq data

11 minute read

Published:

In a previous post, we discussed how RNA-seq provides measurements of relative expression between genes rather than measurements of absolute expression. In this post, we will discuss median-ratio normalization: a procedure that attempts to scale each sample’s read counts so that differences in the read counts between samples better reflects differences in absolute expression. We will start by describing the underlying assumption that must be met for median-ratio normalization to work and then walk through the details of the algorithm.