Matthew N. Bernstein

Matthew N. Bernstein

Computational Biologist at Immunitas Therapeutics

The evidence lower bound (ELBO)

3 minute read

Published:

The evidence lower bound is an important quantity at the core of a number of important algorithms used in statistical inference including expectation-maximization and variational inference. In this post, I describe its context, definition, and derivation.

Introduction

The evidence lower bound (ELBO) is an important quantity that lies at the core of a number of important algorithms in probabilistic inference such as expectation-maximization and variational infererence. To understand these algorithms, it is helpful to understand the ELBO.

Before digging in, let’s review the probabilistic inference task for a latent variable model. In a latent variable model, we posit that our observed data $x$ is a realization from some random variable $X$. Moreover, we posit the existence of another random variable $Z$ where $X$ and $Z$ are distributed according to a joint distribution $p(X, Z; \theta)$ where $\theta$ parameterizes the distribution. Unfortunately, our data is only a realization of $X$, not $Z$, and therefore $Z$ remains unobserved (i.e. latent).

There are two predominant tasks that we may be interested in accomplishing:

  1. Given some fixed value for $\theta$, compute the posterior distribution $p(Z \mid X ; \theta)$
  2. Given that $\theta$ is unknown, find the maximum likelihood estimate of $\theta$:
\[\text{argmax}_\theta l(\theta)\]

where $l(\theta)$ is the log-likelihood function:

\[l(\theta) := \log p(x ; \theta) = \log \int_z p(x, z; \theta) \ dz\]

Variational inference is used for Task 1 and expectation-maximization is used for Task 2. Both of these algorithms rely on the ELBO.

What is the ELBO?

To understand the evidence lower bound, we must first understand what we mean by “evidence”. The evidence, quite simply, is just a name given to the likelihood function evaluated at a fixed $\theta$:

\[\text{evidence} := \log p(x ; \theta)\]

Why is this quantity called the “evidence”? Intuitively, if we have chosen the right model $p$ and $\theta$, then we would expect that the marginal probability of our observed data $x$, would be high. Thus, a higher value of $\log p(x ; \theta)$ indicates, in some sense, that we may be on the right track with the model $p$ and parameters $\theta$ that we have chosen. That is, this quantity is “evidence” that we have chosen the right model for the data.

If we happen to also know (or posit) that $Z$ follows some distribution denoted by $q$ (and that $p(x, z; \theta) := p(x \mid z ; \theta)q(z)$), then the evidence lower bound is, well, just a lower bound on the evidence that makes use of the known (or posited) $q$. Specifically,

\[\log p(x ; \theta) \geq E_{Z \sim q}\left[\log \frac{p(x,Z; \theta)}{q(Z)} \right]\]

where the ELBO is simply the right-hand side of the above inequality:

\[{ELBO} := E_{Z \sim q}\left[\log \frac{p(x,Z; \theta)}{q(Z)} \right]\]

Derivation

We derive this lower bound as follows:

\[\begin{align*}\log p(x; \theta) &= \log \int p(x, z; \theta) \ dz \\ &= \log \int p(x, z; \theta) \frac{q(z)}{q(z)} \ dz \\ &= \log E_{Z\sim q} \left[ \frac{p(x, Z)}{q(z)}\right] \\ &\geq E_{Z\sim q} \left[\log \frac{p(x, Z)}{q(z)}\right]\end{align*}\]

This final inequality follows from Jensen’s Inequality.

The gap between the evidence and the ELBO

It turns out that the gap between the evidence and the ELBO is precisely the Kullback-Leibler divergence between $p(z \mid x; \theta)$ and $q(z)$. This fact forms the basis of the variational inference algorithm for approximate Bayesian inference!

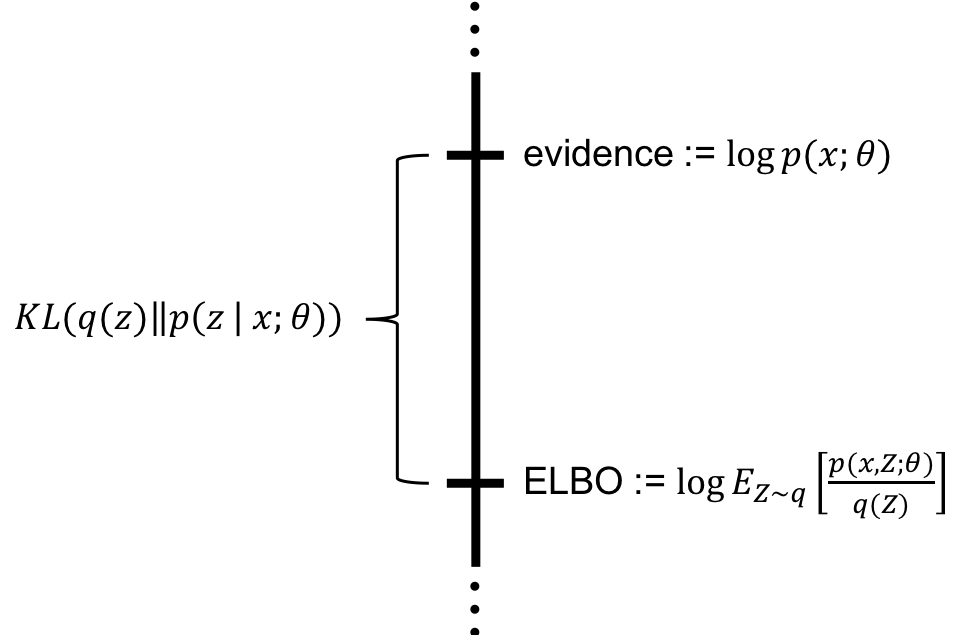
drawing

This can be derived as follows:

\[\begin{align*}KL(q(z) \ \mid \mid p(z \mid x; \theta)) &:= E_{Z \sim q}\left[\log \frac{q(Z)}{p(Z \mid x; \theta)} \right] \\ &= E_{Z \sim q}\left[\log q(Z) \right] - E_{Z \sim q}\left[\log \frac{p(x, Z; \theta)}{p(x; \theta)} \right] \\ &= E_{Z \sim q}\left[\log q(Z) \right] - E_{Z \sim q}\left[\log p(x, Z; \theta) \right] + E_{Z \sim q}\left[\log p(x; \theta) \right] \\ &= \log p(x; \theta) - E_{Z\sim q} \left[\log \frac{p(x, Z; \theta)}{q(z)}\right] \\ &= \text{evidence} - \text{ELBO}\end{align*}\]

You May Also Enjoy

Assessing the utility of data visualizations based on dimensionality reduction

14 minute read

Published:

We human beings use our vision as our chief sense for understanding the world, and thus when we are confronted with data, we try to understand that data through visualization. Dimensionality reduction methods, such as PCA, t-SNE, and UMAP, are approaches designed to enable the visualization of high-dimensional data. Unfortunately, because these methods inevitably distort aspects of the data, these methods are receiving new scrutiny. In this post, I propose that dimensionality reduction requires a “probabilistic” framework of interpretation rather than a “deterministic” one wherein conclusions one draws from a dimensionality reduction plot have some probability of not actually being true of the data. I will propose that this does not mean these plots are not useful. Rather, to evaluate their utility, I will argue that empirical user studies of these methods will shed light on whether these methods provide more benefit or more harm in practice.

The invertible matrix theorem

14 minute read

Published:

Throughout my blog posts on linear algebra, we have proven various properties about invertible matrices. In this post we bring, all of these statements into a single location and form a set of statements called the “invertible matrix theorem”. Each statement in the invertible matrix theorem proves that the matrix is invertible and implies all of the rest of the statements.

Median-ratio normalization for bulk RNA-seq data

11 minute read

Published:

In a previous post, we discussed how RNA-seq provides measurements of relative expression between genes rather than measurements of absolute expression. In this post, we will discuss median-ratio normalization: a procedure that attempts to scale each sample’s read counts so that differences in the read counts between samples better reflects differences in absolute expression. We will start by describing the underlying assumption that must be met for median-ratio normalization to work and then walk through the details of the algorithm.