Matthew N. Bernstein

Matthew N. Bernstein

Computational Biologist at Immunitas Therapeutics

Matrix-vector multiplication

5 minute read

Published:

Matrix-vector multiplication is an operation between a matrix and a vector that produces a new vector. In this post, I’ll define matrix vector multiplication as well as three angles from which to view this concept. The third angle entails viewing matrices as functions between vector spaces

Introduction

In a previous post, we discussed three ways one can view a matrix: as a table of values, as a list of vectors, and finally, as a function. It is the third way of viewing matrices that really gives matrices their power. Here, we’ll introduce an operation between matrices and vectors, called matrix-vector multiplication, which will enable us to use matrices as functions.

Matrix-vector multiplication is an operation between a matrix and a vector that produces a new vector. Notably, matrix-vector multiplication is only defined between a matrix and a vector where the length of the vector equals the number of columns of the matrix. It is defined as follows:

Definition 1 (Matrix-vector multiplication): Given a matrix $\boldsymbol{A} \in \mathbb{R}^{m \times n}$ and vector $\boldsymbol{x} \in \mathbb{R}^n$ the matrix-vector multiplication of $\boldsymbol{A}$ and $\boldsymbol{x}$ is defined as

$$\boldsymbol{A}\boldsymbol{x} := x_1\boldsymbol{a}_{*,1} + x_2\boldsymbol{a}_{*,2} + \dots + x_n\boldsymbol{a}_{*,n}$$

where $\boldsymbol{a}_{*,i}$ is the $i$th column vector of $\boldsymbol{A}$.

Like most mathematical concepts, matrix-vector multiplication can be viewed from multiple angles, at various levels of abstraction. These views come in handy when we attempt to conceptualize the various ways in which we utilize matrix-vector multiplication to model real-world problems. Below are three ways that I find useful for conceptualizing matrix-vector multiplication ordered from least to most abstract:

  1. As a “row-wise”, vector-generating process: Matrix-vector multiplication defines a process for creating a new vector using an existing vector where each element of the new vector is “generated” by taking a weighted sum of each row of the matrix using the elements of a vector as coefficients
  2. As taking a linear combination of the columns of a matrix: Matrix-vector multiplication is the process of taking a linear combination of the column-space of a matrix using the elements of a vector as the coefficients
  3. As evaluating a function between vector spaces: Matrix-vector multiplication allows a matrix to define a mapping between two vector spaces.

I find all three of the perspectives useful. The first two perspectives provide a way of understanding the mechanism of matrix-vector multiplication whereas the third perspective provides the essence of matrix-vector multiplication. It is this third perspective of matrix-vector multiplication that enables us to view matrices as functions, as we discussed in the previous post.

Matrix-vector multiplication as a “row-wise”, vector-generating process

A useful way for viewing the mechanism of matrix-vector multiplication between a matrix $\boldsymbol{A}$ and a vector $\boldsymbol{x}$ is to see it as a sort of “process” (or even as a computer program) that constructs each element of the output vector in an iterative fashion where we iterate over each row of $A$. Specifically, for each row $i$ of $\boldsymbol{A}$, we take $\boldsymbol{x}$ and compute the dot product between $\boldsymbol{x}$ and the $i$th row of the matrix thereby producing the $i$th element of the output vector (See Theorem 1 in the Appendix to this post):

\[\boldsymbol{Ax} = \begin{bmatrix} \boldsymbol{a}_{1,*} \cdot \boldsymbol{x} \\ \boldsymbol{a}_{2,*} \cdot \boldsymbol{x} \\ \vdots \\ \boldsymbol{a}_{m,*} \cdot \boldsymbol{x} \\ \end{bmatrix}\]

where $\boldsymbol{a}_{i,*}$ is the $i$th row-vector in $\boldsymbol{A}$. This process is illustrated schematically in the figure below:

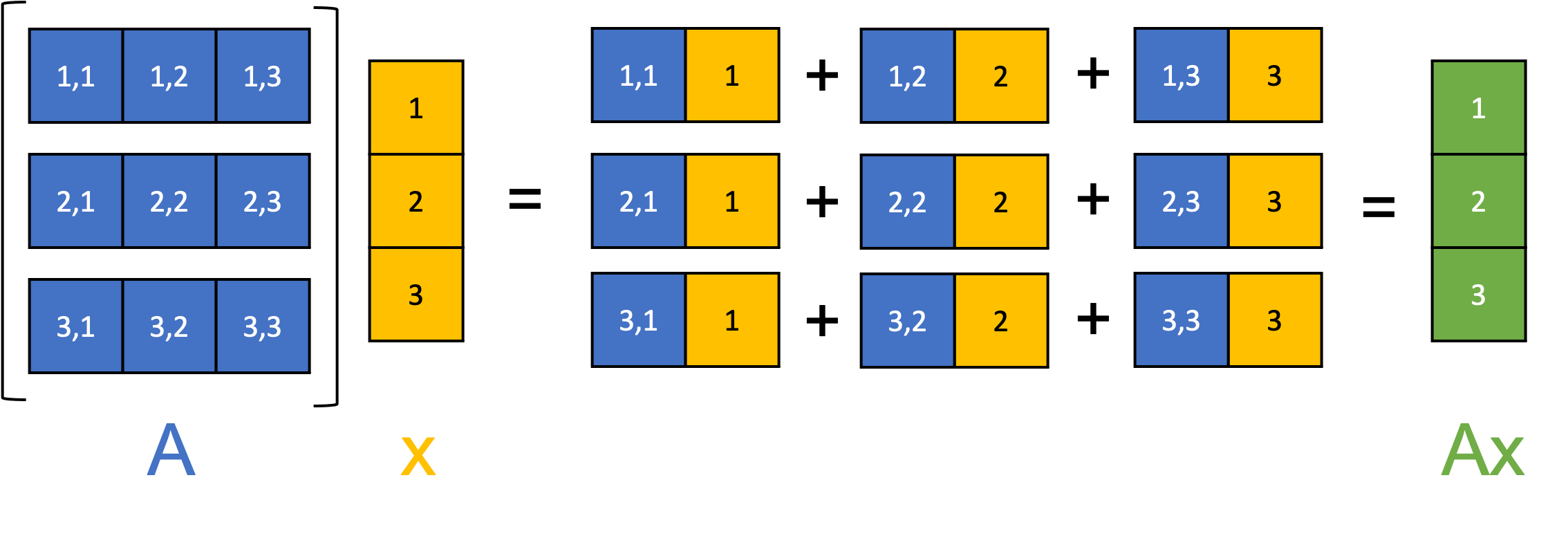
drawing

Matrix-vector multiplication as taking a linear combination of the columns of a matrix

Matrix-vector multiplication between a matrix $\boldsymbol{A} \in \mathbb{R}^{m \times n}$ and vector $\boldsymbol{x} \in \mathbb{R}^m$ can be understood as taking a linear combination of the column vectors of $\boldsymbol{A}$ using the elements of $\boldsymbol{x}$ as the coefficients. This is illustrated schematically below:

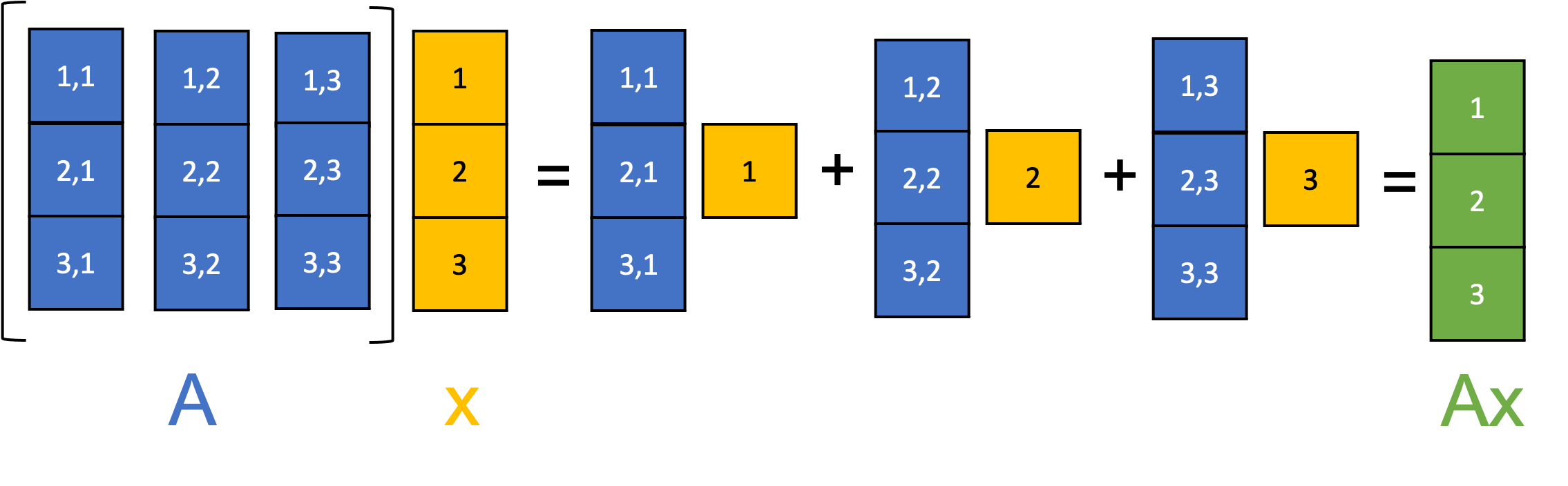
drawing

We can also view this geometrically:

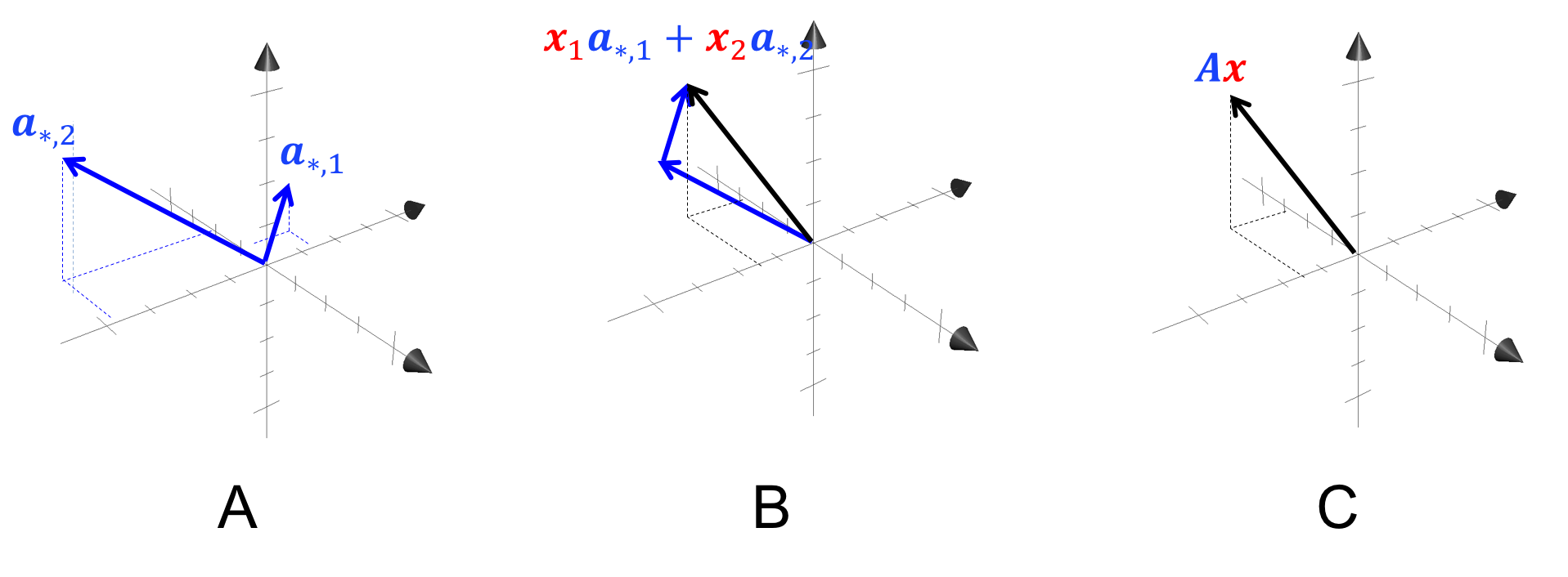
drawing

In Panel A, we depict two column vectors of some matrix $\boldsymbol{A} \in \mathbb{R}^{3,2}$. In Panel B, we take a linear combination of the two column vectors of \(\boldsymbol{A}\) according to the elements of some vector $\boldsymbol{x}$ thus producing the vector $\boldsymbol{Ax}$ (black vector) as shown in Panel C.

Matrix-vector multiplication as evaluating a function between vector spaces

If we hold a matrix $\boldsymbol{A} \in \mathbb{R}^{m \times n}$ as fixed, this matrix maps vectors in $\mathbb{R}^n$ to vectors in $\mathbb{R}^m$. Making this more explicit, we can define a function $T : \mathbb{R}^n \rightarrow \mathbb{R}^m$ as: \(T(\boldsymbol{x}) := \boldsymbol{Ax}\) where $T$ uses the matrix $\boldsymbol{A}$ to performing the mapping.

This is illustrated schematically below:

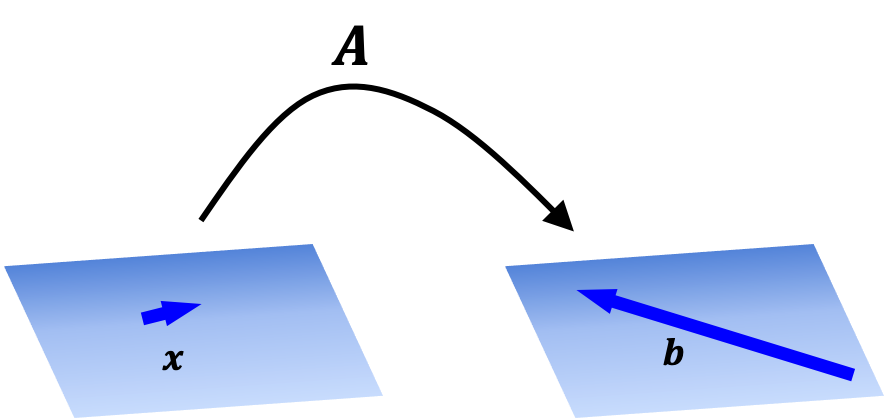
drawing

In fact, as we show in a later post, such a matrix-defined function is a linear function. Even more importantly, any linear function between finite-dimensional vector spaces is uniquely defined by some matrix.

Appendix

Theorem 1: Given a matrix $\boldsymbol{A} \in \mathbb{R}^{m \times n}$ and vector $\boldsymbol{x} \in \mathbb{R}^n$, it holds that

$$\boldsymbol{Ax} = \begin{bmatrix}\boldsymbol{a}_{1,*} \cdot \boldsymbol{x} \\ \boldsymbol{a}_{2,*} \cdot \boldsymbol{x} \\ \vdots \\ \boldsymbol{a}_{m,*} \cdot \boldsymbol{x} \\ \end{bmatrix}$$

where $\boldsymbol{a}_{i,*}$ is the $i$th row-vector in $\boldsymbol{A}$.

Proof:

\[\begin{align*} \boldsymbol{A}\boldsymbol{x} &:= x_1\boldsymbol{a}_{*,1} + x_2\boldsymbol{a}_{*,2} + \dots + x_n\boldsymbol{a}_{*,n} \\ &= x_1 \begin{bmatrix}a_{1,1} \\ a_{2,1} \\ \vdots \\ a_{m, 1} \end{bmatrix} + x_2\begin{bmatrix}a_{1,2} \\ a_{2,2} \\ \vdots \\ a_{m, 2} \end{bmatrix} + \dots + x_n\begin{bmatrix}a_{1,n} \\ a_{2,n} \\ \vdots \\ a_{m, n} \end{bmatrix} \\ &= \begin{bmatrix}x_1a_{1,1} \\ x_1a_{2,1} \\ \vdots \\ x_1a_{m, 1} \end{bmatrix} + \begin{bmatrix}x_2a_{1,2} \\ x_2a_{2,2} \\ \vdots \\ x_2a_{m, 2} \end{bmatrix} + \dots + \begin{bmatrix}x_na_{1,n} \\ x_na_{2,n} \\ \vdots \\ x_na_{m, n} \end{bmatrix} \\ &= \begin{bmatrix} x_1a_{1,1} + x_2a_{1,2} + \dots + x_na_{1,n} \\ x_1a_{2,1} + x_2a_{2,2} + \dots + x_na_{2,n} \\ \vdots \\ x_1a_{m,1} + x_2a_{m,2} + \dots + x_na_{m,n} \\ \end{bmatrix} \\ &= \begin{bmatrix} \sum_{i=1}^n a_{1,i}x_i \\ \sum_{i=1}^n a_{2,i}x_i \\ \vdots \\ \sum_{i=1}^n a_{m,i}x_i \\ \end{bmatrix} \\ &= \begin{bmatrix}\boldsymbol{a}_{1,*} \cdot \boldsymbol{x} \\ \boldsymbol{a}_{2,*} \cdot \boldsymbol{x} \\ \vdots \\ \boldsymbol{a}_{m,*} \cdot \boldsymbol{x} \\ \end{bmatrix}\end{align*}\]

$\square$

You May Also Enjoy

Assessing the utility of data visualizations based on dimensionality reduction

14 minute read

Published:

We human beings use our vision as our chief sense for understanding the world, and thus when we are confronted with data, we try to understand that data through visualization. Dimensionality reduction methods, such as PCA, t-SNE, and UMAP, are approaches designed to enable the visualization of high-dimensional data. Unfortunately, because these methods inevitably distort aspects of the data, these methods are receiving new scrutiny. In this post, I propose that dimensionality reduction requires a “probabilistic” framework of interpretation rather than a “deterministic” one wherein conclusions one draws from a dimensionality reduction plot have some probability of not actually being true of the data. I will propose that this does not mean these plots are not useful. Rather, to evaluate their utility, I will argue that empirical user studies of these methods will shed light on whether these methods provide more benefit or more harm in practice.

The invertible matrix theorem

14 minute read

Published:

Throughout my blog posts on linear algebra, we have proven various properties about invertible matrices. In this post we bring, all of these statements into a single location and form a set of statements called the “invertible matrix theorem”. Each statement in the invertible matrix theorem proves that the matrix is invertible and implies all of the rest of the statements.

Median-ratio normalization for bulk RNA-seq data

11 minute read

Published:

In a previous post, we discussed how RNA-seq provides measurements of relative expression between genes rather than measurements of absolute expression. In this post, we will discuss median-ratio normalization: a procedure that attempts to scale each sample’s read counts so that differences in the read counts between samples better reflects differences in absolute expression. We will start by describing the underlying assumption that must be met for median-ratio normalization to work and then walk through the details of the algorithm.