Matthew N. Bernstein

Matthew N. Bernstein

Computational Biologist at Immunitas Therapeutics

Matrices characterize linear transformations

5 minute read

Published:

Linear transformations are functions mapping vectors between two vector spaces that preserve vector addition and scalar multiplication. In this post, we show that there exists a one-to-one corresondence between linear transformations between coordinate vector spaces and matrices. Thus, we can view a matrix as representing a unique linear transformation between coordinate vector spaces.

Introduction

As previously discussed, matrix-vector multiplication enables us to view matrices as functions between vector spaces. It turns out that matrices define a very specific type of function: linear transformations. In fact, any linear transformation between coordinate vector spaces can be characterized by a single, unique matrix. That is, there is a one-to-one mapping between linear transformations and matrices. Thus, in some sense, we can say that a matrix is a linear transformation.

Linear transformations

A linear transformation is a function that maps vectors from one vector space to vectors in another vector space such that it preserves scaler multiplication and vector addition. Specifically, a linear transformation is defined as follows:

Definition 1 (Linear transformation): Given vector spaces $(\mathcal{V}, \mathcal{F})$ and $(\mathcal{U}, \mathcal{F})$, a function $T : \mathcal{V} \rightarrow \mathcal{U}$ is a linear transformation, or is simply called linear, if for all $\boldsymbol{u}, \boldsymbol{v} \in \mathcal{V}$ and all scalars $c \in \mathcal{F}$,

$$T(\boldsymbol{u} + \boldsymbol{v}) = T(\boldsymbol{u}) + T(\boldsymbol{v})$$

and

$$T(c\boldsymbol{u}) = cT(\boldsymbol{u})$$

The figure below illustrates a linear transformation $T$ applied to three vectors (red, blue, and purple). The vectors on the left are in $T$’s domain and the vectors on the right are in $T$’s range. The dotted lines connect each vector in the domain to its vector in the range as mapped by $T$. Notice that the $T(\text{red}) + T(\text{blue}) = T(\text{red} + \text{blue})$.

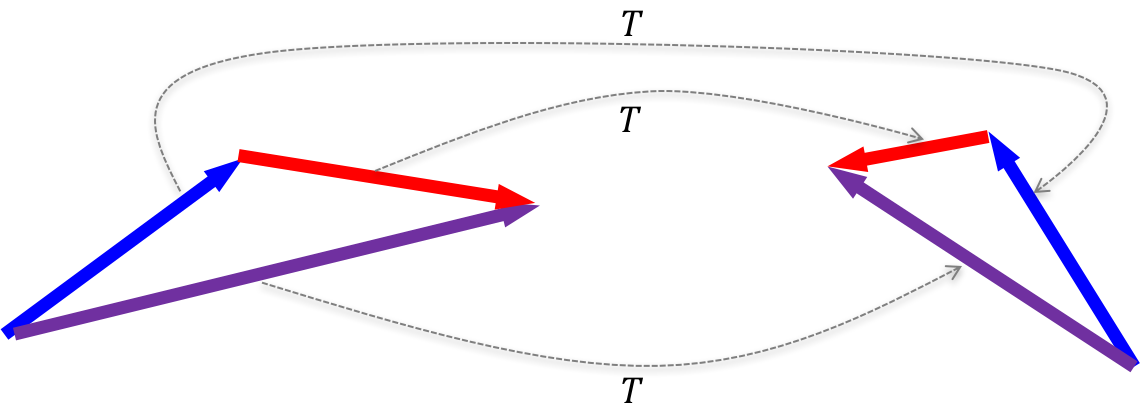
drawing

Matrices perform linear transformations

Matrix-vector multiplication has the following two properties:

  1. $\boldsymbol{A}(\boldsymbol{v} + \boldsymbol{u}) = \boldsymbol{Av} + \boldsymbol{Au}$
  2. $\boldsymbol{A}(c\boldsymbol{v}) = c\boldsymbol{Av}$

Thus, if we hold some matrix $\boldsymbol{A}$ as fixed and define a function $T(\boldsymbol{x}) := \boldsymbol{Ax}$, then it follows that

  1. $T(\boldsymbol{v} + \boldsymbol{u}) = T(\boldsymbol{v}) + T(\boldsymbol{u})$
  2. $T(c\boldsymbol{v}) = cT(\boldsymbol{v})$

That is, $T$ is a linear transformation. These facts are proven in Theorem 1 in the Appendix to this post.

Every linear transformation is characterized by a matrix

Perhaps more interestingly, it turns out that every linear transformation between finite-dimensional vector spaces is defined by a unique matrix that performs the transformation. That is, if I have two vector spaces in, say $\mathbb{R}^m$ and $\mathbb{R}^n$, and I have a linear transformation $T$ mapping vectors between them, then there exists a single unique matrix $\boldsymbol{A}_T$ that performs $T$’s mapping. That is, where $T(\boldsymbol{x}) = \boldsymbol{A}_T\boldsymbol{x}$. This matrix is called the standard matrix of $T$.

Because every matrix performs a linear transformation and every linear transformation is characterized by a matrix, it follows that there is a one-to-one mapping between linear transformations and matrices. Thus, in some sense, we can say that a matrix is is a linear transformation.

Computing the standard matrix of a linear transformation

A natural question is: given a linear transformation $T$, how do we compute its standard matrix? In fact, it’s quite simple. $A_T$ is computed simply as:

\[A_T = \begin{bmatrix}T(\boldsymbol{e}_1) & T(\boldsymbol{e}_2) & \dots & T(\boldsymbol{e}_m) \end{bmatrix}\]

where \(\boldsymbol{e}_i\) is the $i$th basis vector of $\mathbb{R}^m$ (i.e., the vector with every element equal to zero except for the $i$th element, which is equal to one).

What this says is that in order to form the standard matrix for a linear transformation $T$, you simply compute the vectors that result from transforming the basis vectors under $T$. The resultant vectors form the columns of $T$’s standard matrix! This is depicted in the figure below where we visualize the basis vectors for $\mathbb{R}^2$ and the two column vectors of the standard matrix for some linear transformation $T: \mathbb{R}^2 \rightarrow \mathbb{R}^2$:

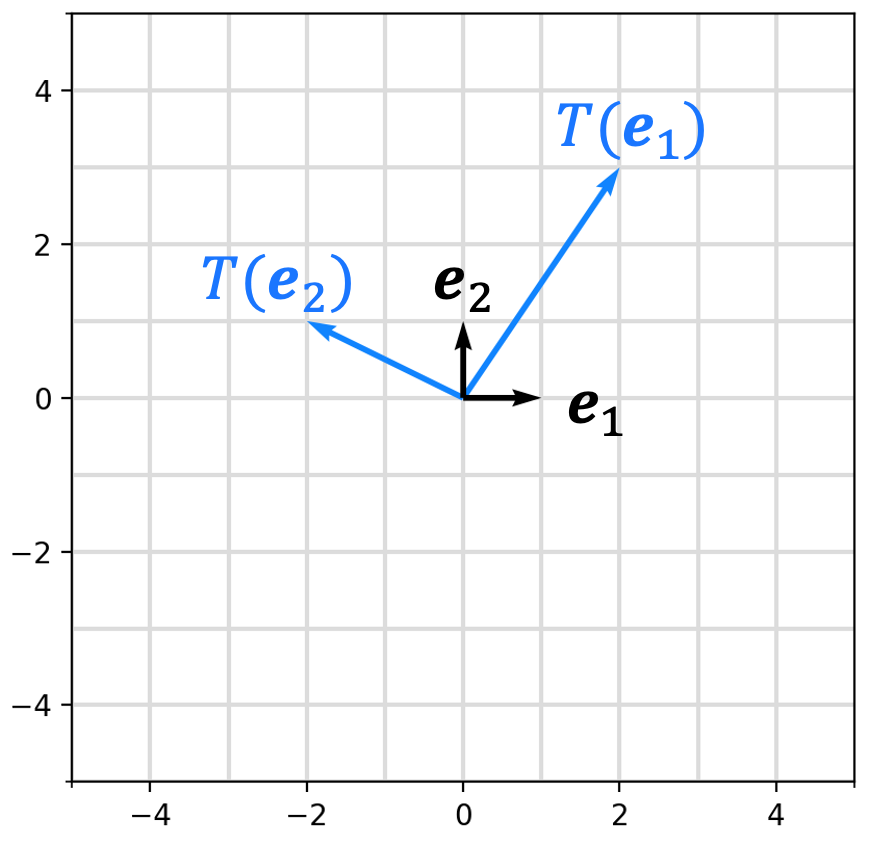
drawing

This is proven in Theorem 2 in the Appendix to this post.

Appendix

Theorem 1 (Matrices define linear transformations): The function $T(\boldsymbol{x}) := \boldsymbol{Ax}$ is a linear transformation.

Proof: We show that for all $\boldsymbol{u}, \boldsymbol{v}$ in the domain of $T$ and for all scalars $c$, the following conditions hold:

  1. $\boldsymbol{A}(\boldsymbol{u} + \boldsymbol{v}) = \boldsymbol{A}\boldsymbol{u} + \boldsymbol{A}\boldsymbol{v}$
  2. $\boldsymbol{A}(c\boldsymbol{u}) = c(\boldsymbol{A}\boldsymbol{u})$

Proof of 1:

\[\begin{align*}\boldsymbol{A}(\boldsymbol{u} + \boldsymbol{v}) &= \boldsymbol{a}_{*,1}(u_1 + v_1) + \boldsymbol{a}_{*,2}(u_2 + v_2) + \dots + \boldsymbol{a}_{*,n}(u_n + v_n) \\ &= \boldsymbol{a}_{*,1}u_1 + \boldsymbol{a}_{*,1}v_1 + \boldsymbol{a}_{*,2}u_2 + \boldsymbol{a}_{*,2}v_2 + \dots + \boldsymbol{a}_{*,n}u_n + \boldsymbol{a}_{*,n}v_n \\ &= (\boldsymbol{a}_{*,1}u_1 + \boldsymbol{a}_{*,2}u_2 + \dots + \boldsymbol{a}_{*,n}u_n) + (\boldsymbol{a}_{*,1}v_1 + \boldsymbol{a}_{*,2}v_2 + \dots + \boldsymbol{a}_{*,n}v_n) \\ &= \boldsymbol{Au} + \boldsymbol{Av}\end{align*}\]

Proof of 2:

\[\begin{align*}\boldsymbol{A}(c\boldsymbol{u}) &= \boldsymbol{a}_{*,1}(cu_1) + \boldsymbol{a}_{*,2}(cu_2) + \dots + \boldsymbol{a}_{*,n}(cu_n) \\ &= c\boldsymbol{a}_{*,1}(u_1) + c\boldsymbol{a}_{*,2}(u_2) + \dots + c\boldsymbol{a}_{*,n}(u_n) \\ &= c(\boldsymbol{a}_{*,1}u_1 + \boldsymbol{a}_{*,2}u_2 + \dots + \boldsymbol{a}_{*,n}u_n) \\ &= c(\boldsymbol{Au})\end{align*}\]

Now, we see that

\[\begin{align*}T(\boldsymbol{u} + \boldsymbol{v}) &= \boldsymbol{A}(\boldsymbol{u} + \boldsymbol{v}) \\ &= \boldsymbol{Au} + \boldsymbol{Av} \\ &= T(\boldsymbol{u}) + T(\boldsymbol{v})\end{align*}\]

and

\[\begin{align*}T(c\boldsymbol{u}) &= \boldsymbol{A}(c\boldsymbol{u}) \\ &= c\boldsymbol{Au} \\ &= cT(\boldsymbol{u})\end{align*}\]

$\square$

Theorem 2 (Standard matrix of a linear transformations): Given a linear transformation $T: \mathbb{R}^m \rightarrow \mathbb{R}^n$, it holds that

$$T(\boldsymbol{x}) = \boldsymbol{A}_T\boldsymbol{x}$$

where $\boldsymbol{A}_T$ is defined as

$$A_T := \begin{bmatrix}T(\boldsymbol{e}_1) & T(\boldsymbol{e}_2) & \dots & T(\boldsymbol{e}_m) \end{bmatrix}$$

where $\boldsymbol{e}_i$ is the $i$th basis vector of $\mathbb{R}^m$.

Proof:

\[\begin{align*} \boldsymbol{x} &= \boldsymbol{Ix} \\ &= \boldsymbol{e}_1x_1, + \boldsymbol{e}_2x_2 + \dots + \boldsymbol{e}_mx_m \\ \implies T(\boldsymbol{x}) &= T(\boldsymbol{e}_1x_1 + \boldsymbol{e}_2x_2 + \dots + \boldsymbol{e}_mx_m) \\ &= T(\boldsymbol{e}_1x_1) + T( \boldsymbol{e}_2x_2) + \dots + T(\boldsymbol{e}_mx_m) && \text{$T$ is linear} \\ &= T(\boldsymbol{e}_1)x_1 + T( \boldsymbol{e}_2)x_2 + \dots + T(\boldsymbol{e}_m)x_m && \text{$T$ is linear} \\ &= \begin{bmatrix} T(\boldsymbol{e}_1) & T(\boldsymbol{e}_2) & \dots & T(\boldsymbol{e}_m) \end{bmatrix} \boldsymbol{x} \\ &= \boldsymbol{A}_T\boldsymbol{x} \end{align*}\]

$\square$

You May Also Enjoy

Assessing the utility of data visualizations based on dimensionality reduction

14 minute read

Published:

We human beings use our vision as our chief sense for understanding the world, and thus when we are confronted with data, we try to understand that data through visualization. Dimensionality reduction methods, such as PCA, t-SNE, and UMAP, are approaches designed to enable the visualization of high-dimensional data. Unfortunately, because these methods inevitably distort aspects of the data, these methods are receiving new scrutiny. In this post, I propose that dimensionality reduction requires a “probabilistic” framework of interpretation rather than a “deterministic” one wherein conclusions one draws from a dimensionality reduction plot have some probability of not actually being true of the data. I will propose that this does not mean these plots are not useful. Rather, to evaluate their utility, I will argue that empirical user studies of these methods will shed light on whether these methods provide more benefit or more harm in practice.

The invertible matrix theorem

14 minute read

Published:

Throughout my blog posts on linear algebra, we have proven various properties about invertible matrices. In this post we bring, all of these statements into a single location and form a set of statements called the “invertible matrix theorem”. Each statement in the invertible matrix theorem proves that the matrix is invertible and implies all of the rest of the statements.

Median-ratio normalization for bulk RNA-seq data

11 minute read

Published:

In a previous post, we discussed how RNA-seq provides measurements of relative expression between genes rather than measurements of absolute expression. In this post, we will discuss median-ratio normalization: a procedure that attempts to scale each sample’s read counts so that differences in the read counts between samples better reflects differences in absolute expression. We will start by describing the underlying assumption that must be met for median-ratio normalization to work and then walk through the details of the algorithm.