Matthew N. Bernstein

Matthew N. Bernstein

Computational Biologist at Immunitas Therapeutics

Matrices as functions

3 minute read

Published:

At the core of linear algebra is the idea that matrices represent functions. In this post, we’ll look at a few common, elementary functions and discuss their corresponding matrices.

Introduction

Recall that the definition of matrix-vector multiplication enables us treat matrices as functions in the following sense: if we hold a matrix $\boldsymbol{A} \in \mathbb{R}^{m \times n}$ as fixed, this matrix maps vectors in $\mathbb{R}^n$ to vectors in $\mathbb{R}^m$. That is, we can define a function $T : \mathbb{R}^n \rightarrow \mathbb{R}^m$ as:

\[T(\boldsymbol{x}) := \boldsymbol{A}\boldsymbol{x}\]

In this post, we’ll look at a few common, elementary functions and discuss their corresponding matrices.

The identity matrix defines the identity function

Recall an identity function $f$ for a set $S$ is the function $f(x) := x$ for all $x \in S$. In the context of a function $T$ over a vector space $\mathbb{R}^n$, the identity function $T(\boldsymbol{x}) := \boldsymbol{x}$ for all $\boldsymbol{x} \in \mathbb{R}^n$ is defined using the identity matrix for $\mathbb{R}^n$. The identity matrix for $\mathbb{R}^n$, denoted $\boldsymbol{I}_n$ (or simply $\boldsymbol{I}$ if the dimensionality is implied by the context), is a square matrix of all zeros except for ones along the diagonal:

Definition 1 (Identity matrix): Each real-valued, Euclidean vector space $\mathbb{R}^n$ is associated with an identity matrix, denoted $\boldsymbol{I}_{n \times n}$ (or simply $\boldsymbol{I}$ if the dimensionality is implied by the context), which is a square matrix consisting of zeros in the off-diagonal entries and ones along the diagonal.

For example, the identity matrix for $\mathbb{R}^3$ is defined as

\[\boldsymbol{I}_3 := \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\]

It can easily be shown that applying matrix-vector multiplication using an identity matrix $\boldsymbol{I}_n$ with any vector $\boldsymbol{x} \in \mathbb{R}^n$ will result in the same vector $\boldsymbol{x}$. Thus, a function $T(\boldsymbol{x}) := \boldsymbol{I}\boldsymbol{x}$ is the identity function with domain $\mathbb{R}^n$. This is depicted schematically below:

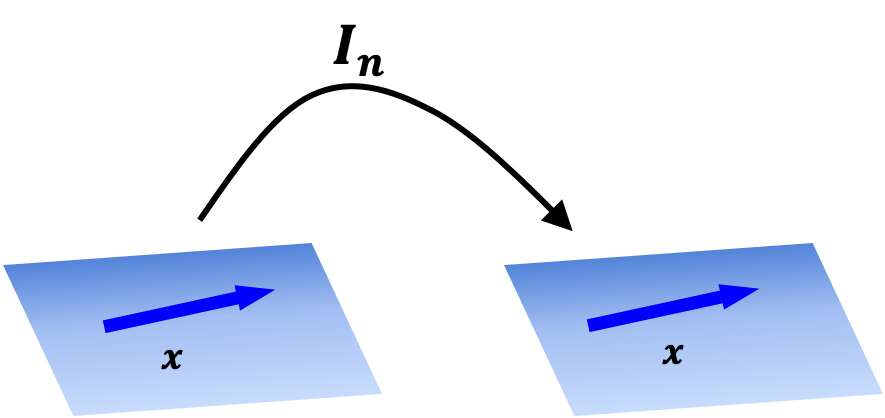
drawing

The zero matrix defines the zero function

Recall a zero-function $f$ for a set $S$ is the function $f(x) := 0$ for all $x \in S$. In the context of a function $T$ over a vector space $\mathbb{R}^n$, the zero function $T(\boldsymbol{x}) := \boldsymbol{0}$ for all $\boldsymbol{x} \in \mathbb{R}^n$ is defined using the zero matrix for $\mathbb{R}^n$. The zero matrix for $\mathbb{R}^n$, denoted $\boldsymbol{0}_n$ is a square matrix of all zeros:

Definition 2 (Zero matrix): Each real-valued, Euclidean vector space $\mathbb{R}^n$ is associated with a zero matrix, denoted $\boldsymbol{0}_{n \times n}$, which is a square matrix consisting of all zeros.

For example, the zero matrix for $\mathbb{R}^3$ is defined as

\[\boldsymbol{0}_3 := \begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}\]

It can easily be shown that applying matrix-vector multiplication using an identity matrix $\boldsymbol{0}_n$ with any vector $\boldsymbol{x} \in \mathbb{R}^n$ will result in the zero vector $\boldsymbol{0}$. Thus, a function $T(\boldsymbol{x}) := \boldsymbol{0}_n\boldsymbol{x}$ is the zero function for domain $\mathbb{R}^n$. This is depicted schematically below:

drawing

An inverse matrix defines an inverse function

Let’s say we have some function $T(\boldsymbol{x}) := \boldsymbol{Ax}$. Let’s say there exists a matrix $\boldsymbol{C}$ such that the function $F(\boldsymbol{x}) := \boldsymbol{Cx}$ is the inverse function of $T$. That is, \(F = T^{-1}\) where

\[T^{-1}(T(\boldsymbol{x})) = \boldsymbol{x}\]

If this is the case, then we call $\boldsymbol{C}$ the inverse matrix of $\boldsymbol{A}$. Usually, we will denote this inverse matrix $\boldsymbol{C}$ as $\boldsymbol{A}^{-1}$. This is depicted in the figure below:

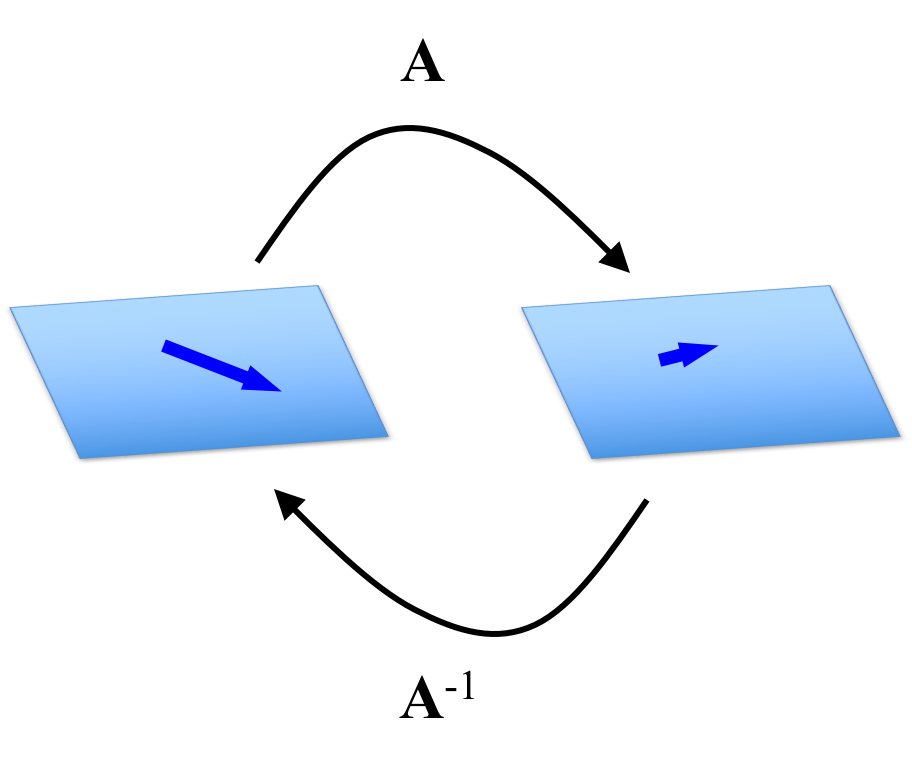
drawing

Not every matrix has an inverse. Matrices that have inverses are a special category of matrix called invertible matrices and have special properties, which we will discuss in a future post.

You May Also Enjoy

Assessing the utility of data visualizations based on dimensionality reduction

14 minute read

Published:

We human beings use our vision as our chief sense for understanding the world, and thus when we are confronted with data, we try to understand that data through visualization. Dimensionality reduction methods, such as PCA, t-SNE, and UMAP, are approaches designed to enable the visualization of high-dimensional data. Unfortunately, because these methods inevitably distort aspects of the data, these methods are receiving new scrutiny. In this post, I propose that dimensionality reduction requires a “probabilistic” framework of interpretation rather than a “deterministic” one wherein conclusions one draws from a dimensionality reduction plot have some probability of not actually being true of the data. I will propose that this does not mean these plots are not useful. Rather, to evaluate their utility, I will argue that empirical user studies of these methods will shed light on whether these methods provide more benefit or more harm in practice.

The invertible matrix theorem

14 minute read

Published:

Throughout my blog posts on linear algebra, we have proven various properties about invertible matrices. In this post we bring, all of these statements into a single location and form a set of statements called the “invertible matrix theorem”. Each statement in the invertible matrix theorem proves that the matrix is invertible and implies all of the rest of the statements.

Median-ratio normalization for bulk RNA-seq data

11 minute read

Published:

In a previous post, we discussed how RNA-seq provides measurements of relative expression between genes rather than measurements of absolute expression. In this post, we will discuss median-ratio normalization: a procedure that attempts to scale each sample’s read counts so that differences in the read counts between samples better reflects differences in absolute expression. We will start by describing the underlying assumption that must be met for median-ratio normalization to work and then walk through the details of the algorithm.