Matthew N. Bernstein

Matthew N. Bernstein

Computational Biologist at Immunitas Therapeutics

Visualizing covariance

1 minute read

Published:

Covariance quantifies to what extent two random variables are linearly correlated. In this post, I will outline a visualization of covariance that helped me better intuit this concept.

Recall that the covariance between two random variables $X$ and $Y$ is defined as

\[\text{Cov}(X, Y) := E[(X-E(X))(Y-E(Y)]\]

When $X$ and $Y$ take on values $x$ and $y$ respectively, we can form a rectangle with sides of length $x − E(X)$ and $y − E(Y)$. The covariance of $X$ and $Y$ is then the expected area of the rectangle with these lengths of sides:

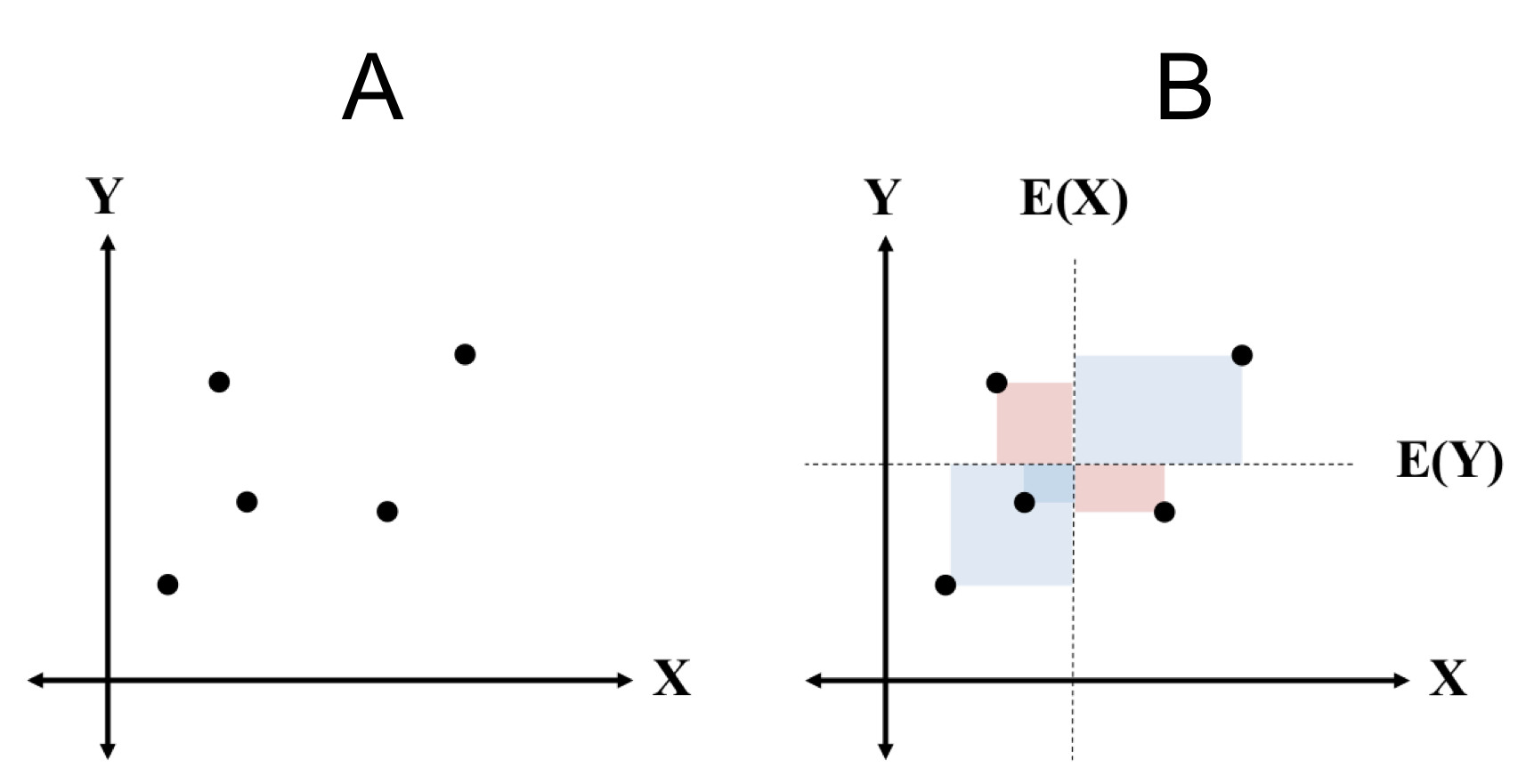
drawing

In part A of the figure above, we depict random samples from the joint distribution $P(X, Y)$. In Part B, we draw rectangles, with sides corresponding to $x − E(X)$ and $y − E(Y)$.

Note, however, that in our discussion, a “length” can have a negative value and thus some rectangles have a “negative area”. Positive-area rectangles correspond to points in which the values of the random variables are either both above or both below their respective means (they “agree”) and negative area rectangles correspond to the situation in which one variable is above it’s mean and the other is below (they “disagree”).

Such a visualization can help in gaining intuition for variance and standard deviation as well. Recall that the variance for a random variable $X$ can be expressed as

\[\text{Var}(X) = \text{Cov}(X, X)\]

Thus, variance can be visualized using the same paradigm:

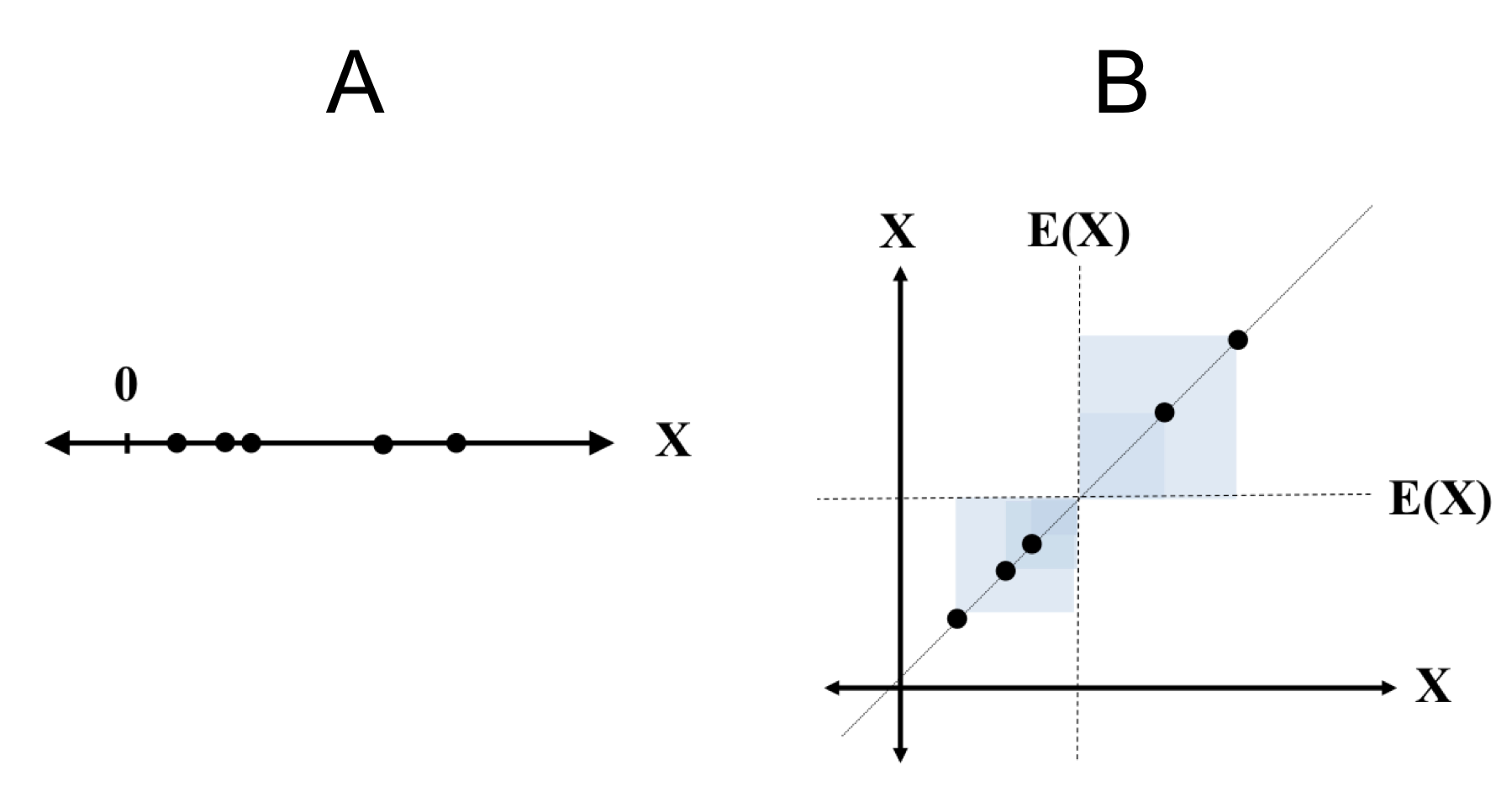
drawing

In Part A of this figure, we depict samples from $X$. In part $B$, we draw a scatterplot plot of each $(x,x)$ with squares of sides length $x - E(x)$.

From this visualization, we can see why variance is always positive: the samples of $X$, when plotted on two axes, will always sit on the line $f(x) = x$.

We also note that the rectangles will always be squares because the sides are equal. Furthermore, when the values of $X$ are more spread out, the areas of the rectangles will be larger and thus, the average size of the rectangles will be a larger number.

Lastly, we note that the standard deviation is simply the length of a side of the average square.

You May Also Enjoy

Assessing the utility of data visualizations based on dimensionality reduction

14 minute read

Published:

We human beings use our vision as our chief sense for understanding the world, and thus when we are confronted with data, we try to understand that data through visualization. Dimensionality reduction methods, such as PCA, t-SNE, and UMAP, are approaches designed to enable the visualization of high-dimensional data. Unfortunately, because these methods inevitably distort aspects of the data, these methods are receiving new scrutiny. In this post, I propose that dimensionality reduction requires a “probabilistic” framework of interpretation rather than a “deterministic” one wherein conclusions one draws from a dimensionality reduction plot have some probability of not actually being true of the data. I will propose that this does not mean these plots are not useful. Rather, to evaluate their utility, I will argue that empirical user studies of these methods will shed light on whether these methods provide more benefit or more harm in practice.

The invertible matrix theorem

14 minute read

Published:

Throughout my blog posts on linear algebra, we have proven various properties about invertible matrices. In this post we bring, all of these statements into a single location and form a set of statements called the “invertible matrix theorem”. Each statement in the invertible matrix theorem proves that the matrix is invertible and implies all of the rest of the statements.

Median-ratio normalization for bulk RNA-seq data

11 minute read

Published:

In a previous post, we discussed how RNA-seq provides measurements of relative expression between genes rather than measurements of absolute expression. In this post, we will discuss median-ratio normalization: a procedure that attempts to scale each sample’s read counts so that differences in the read counts between samples better reflects differences in absolute expression. We will start by describing the underlying assumption that must be met for median-ratio normalization to work and then walk through the details of the algorithm.